En primaire, un instituteur enseigne diverses matières et se doit, pour conserver l'attention des élèves, d'utiliser un maximum de matériel varié ainsi que de maîtriser et d'utiliser diverses méthodes d'enseignement.

Avant toute chose, il me semble important de vous expliquer la manière dont je réalise mes préparations afin de proposer des activités cohérentes (notamment au niveau du programme) et détaillées, que ce soit au niveau de l'analyse-matière, de la méthodologie, des documents des élèves.

Ensuite, il me semble intéressant de montrer dans cette rubrique les différents schémas d'apprentissage que je maîtrise, chacun adapté à une discipline.

Enfin, pour parler des ressources, j'explique en quoi il est intéressant d'utiliser les albums jeunesse dans les apprentissages et je joins un exemple d'activité que j'ai menée à partir d'albums jeunesse. 

La préparation

Pour la préparation, j'ai conçu un modèle vierge de préparation à partir de celui qui nous a été distribué en début d'année par notre pédagogue. J'ai ajouté dans ce modèle (en plus de ma patte graphique), plusieurs sous-points que j'explique ci-dessous afin d'améliorer ma préparation.

1. Intentions pédagogiques

Je note l'intention pédagogique en plusieurs tirets (avec chaque fois un verbe d'action par tiret).

J'ai pensé à faire cela depuis que l'on m'a demandé « Quels sont les objectifs de ta leçon concrètement ? » et que j'avais du mal à répondre car dans ma tête « une phrase = un objectif » malgré la présence de plusieurs verbes d'action dans la phrase.

Je fais d'ailleurs attention à bien utiliser des verbes d'action à chaque fois afin que l'objectif soit concret et vérifiable (notamment par une évaluation).

2. Prérequis

Au départ, je ne faisais pas vraiment attention à cela. Pour moi les prérequis étaient davantage là à titre informatif qu'autre chose. Ce n'est que sur le terrain et grâce à notre cours sur la différenciation que j'en ai compris la réelle utilité.

Je fais désormais attention aux prérequis afin de pouvoir mettre en place des aides pour ceux ne les ayant pas atteints : cartes à tâches, fiches-aide, jeux en autogestion sur ces concepts…

3. Analyse de la matière

En BAC 2 en AFP math, nous avons vu les 3 grands points de l'analyse-matière :

1. Le concept= « Quoi ? » où l'on note toutes les informations sur le concept-matière en lui-même.
2. Les pistes d'apprentissages = « Comment » où je note tous les moyens d'apprendre le concept aux enfants : c'est-à-dire les étapes (pistes méthodologiques) qui vont amener l'élève à rencontrer le concept, le matériel permettant de le rencontrer et les difficultés auxquelles l'élève fera probablement face lors de l'apprentissage.
3. L'intérêt du concept = « Pourquoi » qui est très utile à savoir et surtout à noter au cas où un élève poserait la question « Mais pourquoi on apprend ça ? ». Qui n'a jamais entendu son professeur répondre « Car tu es ici pour apprendre et qu'un jour tu verras tu seras content de l'avoir appris », une réponse qui ne donne nullement sens à l'apprentissage pour l'élève. L'école fondamentale apprend des concepts        « fondamentaux » pour évoluer en société, et il est important que les élèves le sachent, surtout si l'utilité paraît si peu évidente qu'ils posent la question.

Souvent (et je compte continuer à le faire dans ma carrière) je démarre de la fiche vierge recto-verso ici en annexe et je me pose afin de la remplir à la main  en fonction de mes connaissances. Cela peut durer 5, 10 ou 20 minutes. 

A partir de cela je m'informe: je consulte les programmes, je vais à la bibliothèque, je recherche sur internet, je relis mes cours de la discipline concernée... afin d'avoir tout ce qu'il faut pour répondre à chacune de ces questions et être prêt à démarrer la méthodologie en suivant le schéma propre à chaque discipline. Je note alors mes ressources dans la bibliographie.

4. La méthodologie

En fonction de la discipline, je suis le schéma indiqué (cf. article précédent de cette rubrique) avec les 3 grandes phases méthodologiques: mobilisation, apprentissage et exercices. Pour chaque étape, je note les aides, difficultés, points-matière, stratégies des élèves et consignes en suivant un code couleur afin de savoir qu'il y a :

• autant d'aides à énoncer/donner car autant de tirets verts;
• autant de difficultés à cette étape (auxquelles il convient de faire attention) car autant de tirets rouges ;
• autant de points-matière à démontrer car autant de tirets bruns;
• autant de stratégies car autant de tirets bleus;
• autant de consignes à donner car autant de tirets jaunes.

Voici par exemple 3 étapes d'une activité d'éveil reprenant chacun de ces éléments :

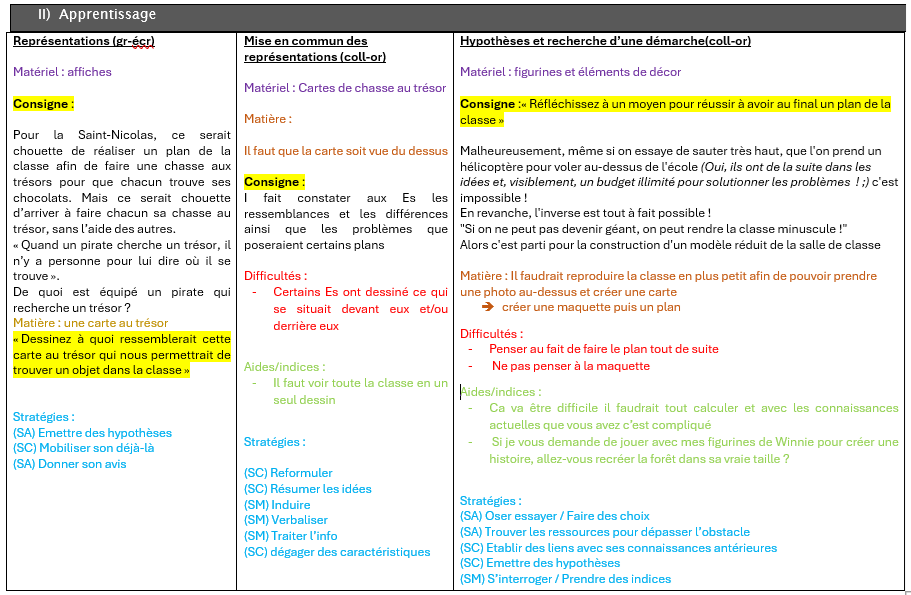
Pour le schéma général d'apprentissage, j'ai déjà prérempli certaines étapes dans mon modèle vierge ci-dessous car des éléments sont récurents dans celles-ci.

Cela permet, d'une part de ne pas devoir renoter les même points à chaque fois et de ne pas les oublier. Par exemple le "conflit socio-cognitif" en phase de groupe qui engendre souvent les même difficultés et aides au niveau de l'entente et donc les même stratégies affectives.

D'autre part, cela permet de savoir à quelle étape noter la matière à apprendre, quelle étape nécessitera probablement la conception de matériel, …

6. Documents des élèves

Après avoir achevé mon déroulement méthodologique (ou en parallèle de celui-ci), je crée les documents des élèves que je place dans un document annexe. Voici 7 types de documents qui reviennent quasiment constamment :

1. Défi : En rapport avec l'auto-socio-constructivisme, j'essaye d'intégrer le plus souvent une situation de défi dans l'apprentissage. Il y a souvent une feuille ou un carnet à compléter (pendant ou après)  quant à la situation-problème.
2. Vérifions ce que l'on a appris… c'est-à-dire la déduction. Ce sont les feuilles où apparaitront des exercices, phrases, situations… qui permettront de confirmer la règle, trouver des exceptions … (cf. schéma d'apprentissage).
3. Dépassement : Il y a presque toujours des élèves plus rapides que ce qui avait été prévu. Au cas-où ces élèves n'auraient pas d'autres exercices/tâches à effectuer en attendant la suite de la leçon, je prévois toujours un petit exercice de dépassement.
4. Synthèse : J'essaye toujours d'intégrer une synthèse, que je n'appelle pas toujours comme cela en fonction de l'activité. Parfois je dis "fiche de procédure", parfois "fiche-aide"... Mais celle-ci garde une importance capitale: certes les élèves ont appris mais c'est bien qu'ils gardent une trace sur laquelle s'appuyer s'ils bloquent ou ont oublié dans le futur
5. Feuilles d'exercices : Rares sont les activités qui ne sont pas suivies d'exercices (en tout cas en math et en français).J'essaye toujours d'en faire quelques uns sur feuille, ceux-ci étant plus faciles à corriger pour constater où se situe l'enfant dans la matière, afin de constituer en conscience le plan de travail pour les centres d'autonomie, comme indiqué à la rubrique "Autonomie".
6. Evaluation : En stage, j'ai rarement effectué des évaluations mais je compte bien en réaliser à l'avenir. Je développe plus largement ce point dans l'article consacré à l'évaluation.
7. Pour les centres d'autonomies : jeux, cartes à tâches, cartes à pinces, QR codes... afin que l'élève puisse s'entraîner pendant l'autogestion, et pas seulement via des exercices sur feuille.

Les schémas d'apprentissage

Dans chaque discipline, nous avons abordé un schéma d'apprentissage permettant aux élèves d'apprendre tout en étant acteurs. Dans ma future carrière, j'essaierai (comme j'ai tenté de la faire à chaque stage) de suivre ces schémas. Ceux-ci ont une place importante pour moi car ils sont en lien avec la logique d'auto-socio-constructivisme (dont je parle dans mon travail d' « élaboration du projet professionnel ») et permettent donc à l'élève d'évoluer en apprenant par lui-même puis en se confrontant aux autres.

Français : le schéma inductif

Le schéma inductif est celui que j'utilisais au départ pour les leçons de toutes les disciplines. C'est grâce à nos différents cours et AFP que j'ai découvert d'autres manières de faire pour chaque discipline , dont l'éveil et les maths (expliqués ci-dessous). Cependant, en français, je considère que ce schéma inductif est toujours le plus approprié, que ce soit pour découvrir une règle d'orthographe, de grammaire, de conjugaison…

Je démarre donc par la mobilisation avec une situation-problème qui donnera envie aux enfants d'apprendre la nouvelle notion (faire une recette, faire une poésie ou une chanson à la manière de…). Je propose alors un défi démarrant de l'analyse de mon support pour la situation-problème (ex : classe tous les verbes de la chanson).

A partir de ce défi vient la phase d'apprentissage. Lors de celle-ci, le schéma inductif me permet de mener un apprentissage auto-socio-constructiviste car l'élève démarre d'abord par une recherche individuelle qui leur permet de réfléchir par lui-même. C'est la phase « auto ».

Ensuite vient la phase de confrontation par groupe dans lequel l'élève va confronter les résultat de sa recherche avec ceux des autres. Cela permet un conflit socio-cognitif, qui entraîne l'utilisation de nouvelles compétences transversales et de nouvelles stratégies comme la remise en question, la coopération… En fonction des activités, je varie les groupes en créant parfois des groupes de niveaux homogènes (en demandant aux groupes plus doués dans la matière d'aller plus loin dans leur réflexion) ou au contraire des groupes de niveaux hétérogènes (pour permettre aux élèves les plus doués d'aider ceux qui s'en sortent moins bien). J'essaie également de prévoir régulièrement des activités dans lesquelles ils choisissent leurs groupes pour favoriser l'engagement. Parfois, une meilleure entente de base entre les élèves permet une discussion plus créative, dans laquelle l'élève a moins peur de s'exprimer.

Nous mettons alors en commun les découvertes de chaque groupe, soit via la présentation d'une affiche réalisée par chaque groupe, soit par un tour de table. J'essaie toujours que ce moment soit le moins « frontal » possible et de tirer un maximum de ce que les enfants ont appris. Souvent l'induction se fait en même temps que la mise en commun, car on construit le « puzzle » (= la règle) à partir de chaque pièce (=élément de réponse) apportée par les enfants.

Vient alors la déduction, pour laquelle je donne une nouvelle feuille, de nouveaux mots/éléments à analyser/classer afin de confirmer la règle et de trouver les exceptions s'il y en a. Parfois, certaines exceptions sont déjà vues lors de l'induction en fonction de la situation-problème (par exemple les verbes être et avoir qui reviennent souvent). J'essaye que cette déduction soit individuelle afin de vérifier que chaque enfant ait bien compris et de pouvoir mettre en place une remédiation, si besoin, avant le début de la phase d'exercices/ateliers autonomes/ évaluations formatives.

Grâce à tout ce qui a été appris, nous réalisons alors une synthèse contenant la règle et les exceptions afin de pouvoir revenir à la situation-problème et créer soi-même sa recette, sa poésie/chanson à la manière de…

Mathématiques : du concret à l'abstrait

En mathématiques, j'applique aussi le schéma inductif (mobilisation à recherche individuelle à confrontation à mise en commun et induction à déduction) mais je décompose la leçon en 4 stades pour « respecter les stades mathématiques », chaque stade ayant son importance pour arriver à ce que l'enfant comprenne la notion mathématique (nombre, calcul, formule, fraction…). Pour illustrer ma manière de faire, je vous propose en exemple (entre parenthèses) les étapes de la (re)découverte de l'ordre et de l'imbrication des nombres grâce aux réglettes Cuisenaire en lien avec mes personnages de Winnie l'Ourson dont je parle dans l'article « Winnie et Cuisenaire » de la rubrique « Pensée innovante ».

• Le stade concret permet à l'élève de manipuler un matériel « non-mathématique », c'est à dire un matériel de la vie de tous les jours (exemple : ordre de grandeurs des peluches de Winnie). Cela permet, en plus de faire vivre sensoriellement l'activité, de faire le lien entre la vie quotidienne de l'enfant et les mathématiques et, donc, de créer du sens.
• Lors du stade semi-concret, l'enfant manipule un matériel « mathématique » didactique épuré qui n'est pas un objet de la vie de tous les jours mais un objet conçu pour l'apprentissage des mathématiques (exemple : manipuler les réglettes Cuisenaire et voir l'ordre de grandeurs), qui permet d'observer la notion dans toute sa complexité et, à terme, de comprendre chacun de ses aspects/règles et la démarche de résolution.
• L'enfant représente ensuite le matériel manipulé (exemple : dessiner les réglettes sur des feuilles avec un quadrillage d'1cm²) et pourra faire le lien avec les nombres notés en chiffres sur cette même feuille (abstrait).
• Le stade abstrait (ex: noter les nombres dans l'ordre croissant, en chiffres) se retrouve donc nettement simplifié suite aux nombreuses images mentales qui se sont ancrées chez l'enfant lors des manipulations et représentations précédentes.

Chaque stade aura permis à l'enfant de verbaliser et de découvrir du vocabulaire pertinent grâce au matériel semi-concret (représenté en semi-abstrait).

J'utiliserai donc encore cette méthode dans ma carrière car c'est celle qui donne le plus de sens aux mathématiques.

Cette logique est en concordance avec les 10 principes du « Math et Sens » (série de livres co-écrits par Mme Van Pachterbeke, notre professeur de mathématiques) ainsi que le document « Méthodologie spéciale : mathématiques » qui nous a été partagé en BAC1 par nos pédagogues (Mme Balaes et Mme Guerriat).

Eveil : le schéma de l'éveil

J'attache beaucoup d'importance au schéma de l'éveil car il correspond parfaitement à mon ikigaï (rubrique « Qui suis-je ») qui est "éveilleur". Même si cela est difficile et demande une grande mise en place, j'essaye de respecter au maximum les étapes pour éveiller la curiosité de l'élève à travers des expériences qu'il retiendra longtemps et pour lui donner envie d'en découvrir toujours plus sur le monde qui l'entoure (histoire et patrimoine, fonctionnement d'un élément technologique, comprendre le monde naturel, paysages…). J'aimerais, à travers mes activités d'éveil, que l'école soit un moteur de curiosité chez l'élève. J'illustre ici les étapes à l'aide de la leçon « maquette de la classe » que j'ai menée en stage spécialisé.

Pour la mobilisation, j'essaye de partir de l'observation d'un fait insolite (ex : après quelques instants, on ne voit plus l'eau qui a permis d'effacer le tableau) et de faire en sorte que les élèves se posent des questions.

A partir de toutes les questions que l'on se pose, on en choisit une (ex : comment l'eau change d'état) et chacun dit/note ses représentations soit à l'oral (chez les petits) soit à l'écrit avec une affiche (chez les grands). On met alors en commun nos représentations et on formule nos hypothèses (ex : il faut chauffer ou refroidir l'eau pour qu'elle change d'état).

Pour confirmer ces hypothèses, on réfléchit à une démarche nous permettant de répondre à notre questions. Il s'agira alors soit de recherche documentaire soit d'expériences. Personnellement, j'essaye toujours, si c'est possible, que les élèves réalisent des expériences (ex : ébullition, eau au congélateur, la buée sur les vitres…) ou du moins des manipulations . Les expériences peuvent être de différents types : à suivre (suivre un protocole), défi (arriver à un résultat demandé en utilisant le matériel à disposition), pour ressentir (on utilise ses sens pour découvrir le phénomène)… On peut noter ses observations/conclusions dans un carnet et effectuer ensuite la mise en commun et une synthèse.

Je joins ici la liste des expériences effectuées, la mise en commun, le carnet et la synthèse (je ne mets pas toute la préparation car, les enfants n'ayant pas encore vu les états de la matière, une étape s'est ajoutée et a modifié le schéma d'éveil).

De la même manière, il existe également d'autres pédagogies spécifiques comme celle de religion (dont je parle et donne un exemple dans l'article "Leçon sur le pardon" de la rubrique "Communication" ) et je pense donc qu'il est toujours bon (et je fais mon maximum pour) d'adapter le schéma méthodologique de ses leçons en fonction du déroulement que nous conseille le programme (comme pour religion) et des schémas qui font consensus chez nos pédagogues (comme le schéma inductif) et/ou mentionnés dans différents livres (comme le "Math et Sens" pour les mathématiques).

J'essaye donc toujours de comparer ma manière de faire (en fonction des savoirs que je maîtrise) aux différentes ressources disponibles.

Littérature jeunesse

Pour être honnête, comme je l'ai brièvement évoqué dans mon travail d'élaboration du projet professionnel dans la rubrique "Qui suis-je ?" je n'ai jamais été un très grand lecteur, et encore moins d'albums jeunesse.

Cependant, de par la nature de mes études, j'ai fini par m'y intéresser et surtout par découvrir la richesse pédagogique que la littérature jeunesse apporte.

En effet, l'utilisation d'un album jeunesse dans le cadre scolaire comporte de multiples avantages.

Premièrement, la découverte d'un album jeunesse provoque souvent plus d'enthousiasme chez l'élève que la découverte d'une feuille-défi. Celui-ci est impatient de découvrir l'histoire et y met souvent plus de volonté. Cela crée aussi une image mentale puissante chez l'enfant qui se rappellera plus facilement d'un élément enrobé dans une histoire que lors d'un apprentissage classique. Lors d'un insight (indices lors de la recherche), l'éclair de génie survient parfois lorsqu'on dit (souviens-toi, c'est comme ce qu'on a vu dans l'album...)

Ensuite, d'une manière générale, les albums jeunesse permettent de développer plusieurs compétences en savoir-lire et savoir-écouter:

• Inférence (liens entre les différentes pages)
• Développement du vocabulaire
• Découverte des rapports texte-image (à laquelle j'ai d'ailleurs consacré une leçon que je place sous la rubrique avec certaines explications).

• Découverte du schéma narratif

Enfin, un grand nombre d'albums jeunesse ont un intérêt supplémentaires par rapport à ce qui est cité ci-dessus. Cela peut se situer dans une autre branche du français mais aussi dans une branche des mathématiques, de l'éveil...

Mes albums personnels, je les classe par discipline et y colle une petite étiquette de couleur (voir "couleurs de rangement" dans la rubrique "Esprit critique" sur le bord de l'album afin de me souvenir de la discipline concernée.

Pour le cycle 3 et 4, je n'ai pas vraiment testé la littérature jeunesse mais pour le cycle 2 (pour mon stage en P1) je savais que les élèves étaient particulièrement émerveillés par les histoires et avaient envie d'en découvrir. Voici une liste (co-créée avec Céline Gillet et Charlotte Bakalarz suite à nos stages de P1 et nos différentes expériementations) des albums jeunesses classés par discipline et l'intérêt d'utiliser chacun d'entre eux.

Prépa rapport texte-image

Cette prépa a été conçue pour les P1 à partir du livre Défi Lire: 6 à 8 ans aux éditions Accès. Ce livre permet de réaliser des activités autour du livre pour les enfants qui ne savent pas encore très bien lire, sans faire de bain de lecture. Il y introduit le vocabulaire lié au livre (couverture, auteur, titre...), le rapport texte-image, les albums sans texte, les contes, les différents points de vue du narrateur (1e personne, 3e personne, omniscient...). 

Personnellement, j'ai donc pris plaisir à voir le rapport texte-image avec ce livre. Chaque jour pendant une semaine et demi nous avons pu découvrir un livre et un nouveau rapport texte-image (ou un nouvel exemple d'un rapport déjà vu) à travers un jeu de questions-réponses avec les élèves qui les incitaient à faire attention aux détails de l'histoire, tant dans les textes que dans les images. 

Les meilleurs moments se passaient lorsque le texte contredisait l'image (rapport de disjonction), par exemple avec l'album "mon chat le plus bête du monde" qui dit "chat" dans le texte mais dont les images montrent un éléphant.

Des leçons comme celles-ci m'incitent à trouver des manuels qui proposent une méthodologie qui engage les élèves, donnent du sens à leur apprentissage et leurs donnent envie d'être curieux, comme je l'ai dit dans l'article ci-dessus "le schéma d'apprentissage de chaque discipline" avec le "Math et sens. Merci donc à ma maître de stage de P1 pour cette découverte.